De la physique dans une chope de bière, pourquoi pas ? Mais penser à la décroissance radioactive en regardant disparaître l’épaisseur de mousse, ça vous semble aberrant ? Eh bien, ce clip vous prouvera que non.
Fiche d’accompagnement de l’expérience:
La diminution de l’épaisseur de mousse dans un verre de bière peut être utilisée pour simuler la décroissance exponentielle de la radioactivité naturelle.
 Matériel
Matériel-
une éprouvette graduée haute et large ou un verre plutôt large et de section constante ;
-
une bouteille ou une boîte de bière, de 50 cl ;
-
un double décimètre ;
-
accessoires : règle, ruban adhésif, crayon.
 Montage et réalisation
Montage et réalisationLaver soigneusement un verre de forme haute afin d’éliminer toute trace de détergent pour la vaisselle. Prendre de préférence un verre large afin que la mousse n’adhère pas trop aux parois : ce phénomène gênerait la baisse du niveau de la mousse lors de sa disparition ou empêcherait de distinguer le niveau exact de la mousse. Le récipient doit être débarrassé de traces résiduelles de détergent car celles-ci « cassent » la mousse et gênent considérable-ment les mesures.
Essuyer la partie extérieure du verre et y coller une bande de papier allant du fond du verre jusqu’au bord supérieur. On peut aussi placer contre la paroi du verre le double décimètre maintenu en position verticale.
Verser rapidement la bière dans le verre en tenant la bouteille à 30 cm au moins au dessus du verre. Il faut obtenir une épaisseur de mousse la plus grande possible (voir figure 1). A priori toutes les sortes de bières conviennent, pourvu qu’elles soient utilisées à température ambiante pour favoriser la création de mousse.
A intervalles de temps réguliers (toutes les 5 secondes au début de l’expérience, de 10 à 20 secondes ensuite), il faut relever sur le double décimètre les deux niveaux de la couche de mousse, ou plus simplement repérer le niveau supérieur et le niveau inférieur de la mousse par un trait au crayon porté sur la bande de papier. Attention : le niveau supérieur ET le niveau inférieur de la mousse varient. L’expérience est terminée lorsque les niveaux de mousse ne changent pratiquement plus. Calculer alors l’épaisseur de la couche de mousse, par soustraction des mesures précédentes. Lorsqu’on porte sur un diagramme cette épaisseur en fonction du temps, on obtient une courbe exponentielle (figure 2).
 Explications
ExplicationsLa pression à l’intérieur des bulles de la mousse est supérieure à la pression atmosphérique (la surpression dans les bulles est régie par la loi de Laplace : la pression y est inversement proportionnelle au rayon de la bulle). Au cours du temps le liquide est entraîné vers le bas de la bulle par son poids. Ceci engendre des défauts d’homogénéité dans l’épaisseur de la paroi de la bulle. L’excès de pression peut induire la rupture de la bulle au niveau de ces défauts.
Le liquide libéré par les bulles qui ont éclaté s’accumule dans le fond du récipient. Si l’on admet que toutes les bulles ont la même probabilité 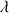 d’éclater, on peut en déduire que le nombre
d’éclater, on peut en déduire que le nombre 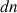 de bulles qui éclatent pendant l’intervalle de temps
de bulles qui éclatent pendant l’intervalle de temps 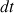 est :
est :
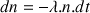 (où
(où  est le nombre total de bulles à l’instant
est le nombre total de bulles à l’instant 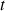 ).
).
Ce qui donne par intégration :
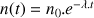 (avec
(avec 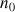 le nombre de bulles au début de la mesure).
le nombre de bulles au début de la mesure).
Si l’on porte sur un diagramme la hauteur de la mousse (qui est proportionnelle au nombre de bulles) en fonction du temps, on obtient ainsi une exponentielle.
Sur la figure 2 on voit la courbe obtenue avec la couche de mousse filmée dans la vidéo, en prenant les mesures toutes les 5 secondes jusque t = 30 s, toutes les 10 secondes jusque t = 80 s, et toutes les 20 secondes ensuite. Un ajustement réalisé avec une fonction exponentielle restitue bien la courbe obtenue, avec une constante de décroissance de 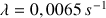
 Remarques
RemarquesDe nombreux phénomènes, dans des domaines variés de la physique, se modélisent par une loi en exponentielle décroissante. Le plus connu d’entre eux est la radioactivité naturelle de l’isotope 14 du carbone, utilisée pour dater des échantillons très anciens : Lorsqu’une plante ou un animal est vivant, son organisme échange du carbone avec son environnement, si bien que le carbone qu’il contient a la même proportion de carbone 14 que dans la biosphère, qui est connue (le rapport 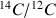 , très faible, est évalué à
, très faible, est évalué à 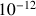 ). Lorsque l’organisme meurt, il ne reçoit plus de
). Lorsque l’organisme meurt, il ne reçoit plus de 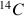 et celui qu’il contient va se désintégrer peu à peu, en suivant une loi exponentielle ; la constante
et celui qu’il contient va se désintégrer peu à peu, en suivant une loi exponentielle ; la constante 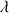 qui figure dans l’exposant correspond à une demi-vie (temps pour lequel le nombre de particules radioactives décroît de moitié) valant 5730 ans (plus ou moins 40 ans). En mesurant le rapport
qui figure dans l’exposant correspond à une demi-vie (temps pour lequel le nombre de particules radioactives décroît de moitié) valant 5730 ans (plus ou moins 40 ans). En mesurant le rapport 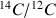 avec un spectromètre de masse, on peut ainsi dater l’âge de l’échantillon. Cette technique permet de remonter jusqu’à 40 000 ans après la mort de l’organisme.
avec un spectromètre de masse, on peut ainsi dater l’âge de l’échantillon. Cette technique permet de remonter jusqu’à 40 000 ans après la mort de l’organisme.

